报告地点：舜耕校区实验楼505

报告时间：2025年10月17日（星期五）9:30—11:30

主办单位：日本做爱

协办单位：科研处，黄河流域生态统计协同创新中心，现代统计交叉科学重点实验室，统计学博士后科研流动站

一、青年教师工作论文报告

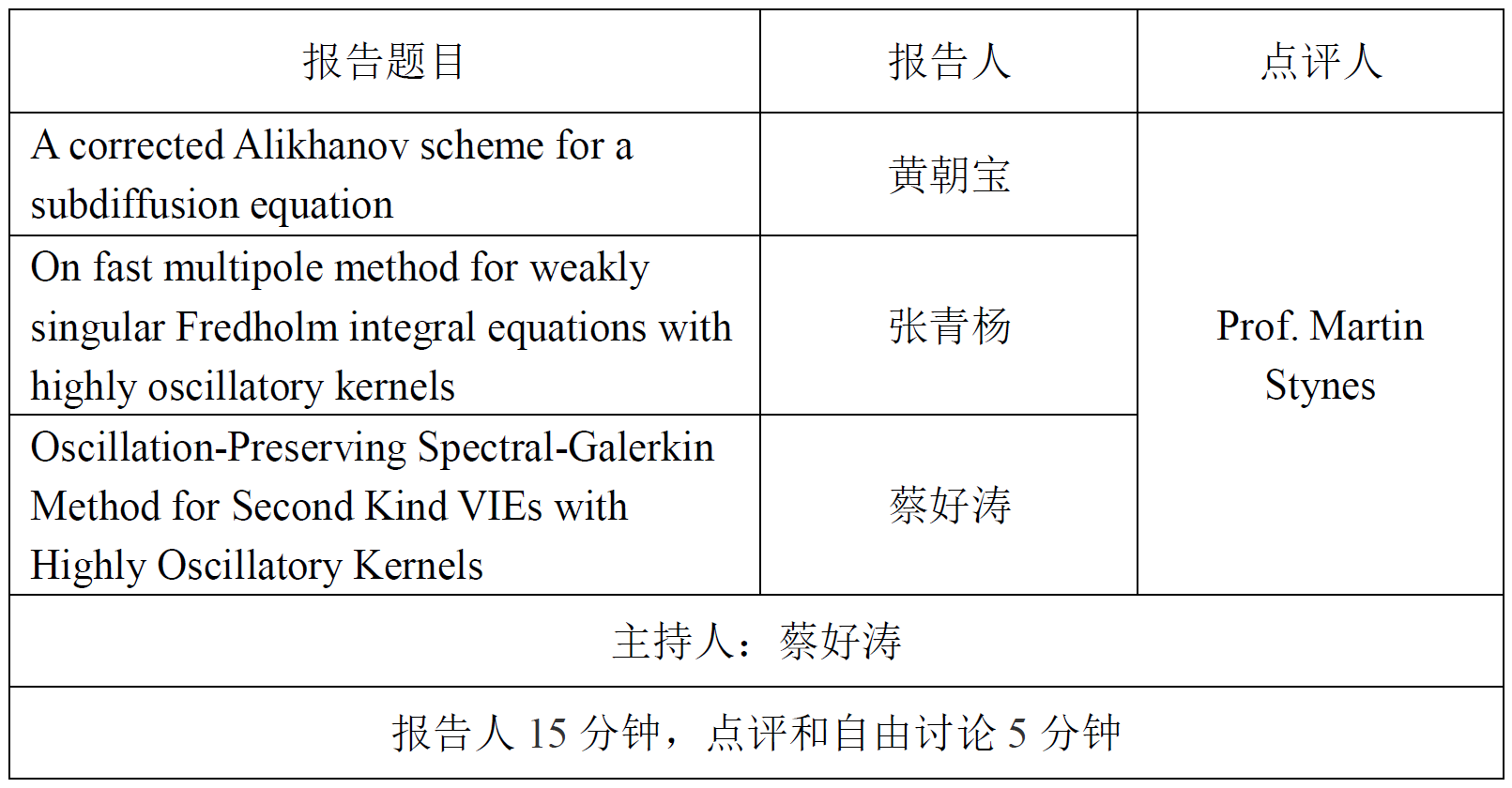
二、特邀专家报告

报告题目：Compatibility of collocation error analyses for Volterra integral equations with smooth and weakly singular kernels

报告人：Prof. Martin Stynes, Beijing Science Researcher Center

报告人简介：Martin Stynes obtained his B.Sc and M.Sc. degrees from University College Cork, Ireland, then his PhD degree from Oregon State University, USA in 1977. After some other positions, he was at University College Cork from 1984 to 2012. Since 2013 he has been at Beijing CSRC. He has worked for many years on the numerical solution of singularly perturbed differential equations; the book on this topic by Roos, Stynes and Tobiska is the standard international reference work (1st edition 1996, 2nd edition 2008). For the last 5 years he has worked mainly on fractional-derivative differential equations and their numerical solution. He is an editor of the journals Advances in Computational Mathematics, Journal of Scientific Computing, Fractional Calculus and Applied Analysis, and Computational Methods in Applied Mathematics.

报告摘要：The numerical solution by piecewise polynomial collocation and iterated collocation of Volterra integral equations (VIEs) of the second kind has been extensively studied and apparently sharp convergence results are known for the cases of a smooth kernel K(t,s) and a weakly singular kernel (t-s)^{-α}K(t,s), where α∈(0,1) is a parameter. If one takes the formal limit as α→0, then the weakly singular VIE reduces to the smooth VIE, but the known collocation error bounds for the weakly singular VIE do not become the collocation error bounds for the smooth VIE —— the error bounds for the smooth VIE are typically of a higher order. In the current paper this anomaly is explained and new sharper collocation and iterated collocation error bounds are derived for the weakly singular VIE that blend exactly as α→0 with known error bounds for the smooth VIE. This analysis is substantially different from previous VIE collocation analyses, e.g., it constructs a remarkable new decomposition of the solution of the weakly singular VIE, it investigates in detail the dependence on α of the matrices associated with collocation, it establishes a new Gronwall inequality, and the dependence of the error on the parameter α is traced precisely throughout the work.